1. K-means算法
k-means算法是机器学习中常用的聚类算法,原理简单实现容易,内存占用量也比较小。但使用这个方法时,需要事先指定将要聚合成的簇数![]() 。
。
在先验知识缺乏的情况下,想要确定![]() 是非常困难的。
是非常困难的。
目前常用的用来确定![]() 的方法主要有两种:肘部法、轮廓系数法。
的方法主要有两种:肘部法、轮廓系数法。
2. 初始k值的选择
1) 肘部法
肘部法所使用的聚类评价指标为:数据集中所有样本点到其簇中心的距离之和的平方。但是肘部法选择的并不是误差平方和最小的![]() ,而是误差平方和突然变小时对应的
,而是误差平方和突然变小时对应的![]() 值。
值。
2) 轮廓系数法
轮廓系数是一种非常常用的聚类效果评价指标。该指标结合了内聚度和分离度两个因素。其具体计算过程如下:
假设已经通过聚类算法将待分类的数据进行了聚类,并最终得到了![]() 个簇。
个簇。
对于每个簇中的每个样本点![]() ,分别计算其轮廓系数。
,分别计算其轮廓系数。
具体地,需要对每个样本点![]() 计算以下两个指标:
计算以下两个指标:
![]() :样本点
:样本点![]() 到与其属于同一个簇的其他样本点的距离的平均值。
到与其属于同一个簇的其他样本点的距离的平均值。
![]() 越小,说明该样本
越小,说明该样本![]() 属于该类的可能性越大。
属于该类的可能性越大。
![]() :样本点
:样本点![]() 到其他簇
到其他簇![]() 中的所有样本的平均距离
中的所有样本的平均距离![]() 的最小值 ,
的最小值 ,![]()
则样本点![]() 的轮廓系数为:
的轮廓系数为:
![]()
而所有样本点![]() 的轮廓系数的平均值,即为该聚类结果总的轮廓系数
的轮廓系数的平均值,即为该聚类结果总的轮廓系数 。
。
 ,
, 越接近与1,聚类效果越好。
越接近与1,聚类效果越好。
3) 具体案例
先利用sklearn.datasets中的方法生成自己的聚类数据集。
具体如下:

对数据x进行归一化(因为KMeans算法中涉及到距离的计算),具体如下:

使用肘部法确定![]() 值,其代码如下:
值,其代码如下:

使用轮廓系数确定![]() 值,其代码如下:
值,其代码如下:

总结
以上为个人经验,希望能给大家一个参考,也希望大家多多支持。
© 版权声明
THE END
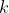









暂无评论内容