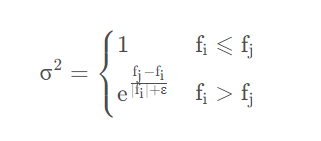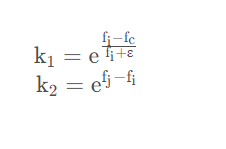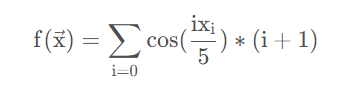算法简介
鸡群算法,缩写为CSO(Chicken Swarm Optimization),尽管具备所谓仿生学的背景,但实质上是粒子群算法的一个变体。
简单来说,粒子群就是一群粒子,每个粒子都有自己的位置和速度,而且每个粒子都要受到最佳粒子的吸引,除了这两条规则之外,粒子之间完全平等,彼此之间除了位置和速度之外,完全相等。
当然,粒子群算法本身也是有仿生学背景的,据说灵感来自于鸟群觅食,这个当然不重要,无非是一群平等的粒子变成了一群平等的鸟罢了。
而鸡群算法,则是为这些粒子,或者这些鸟,添加了不同的身份特征,使得彼此之间不再等同。
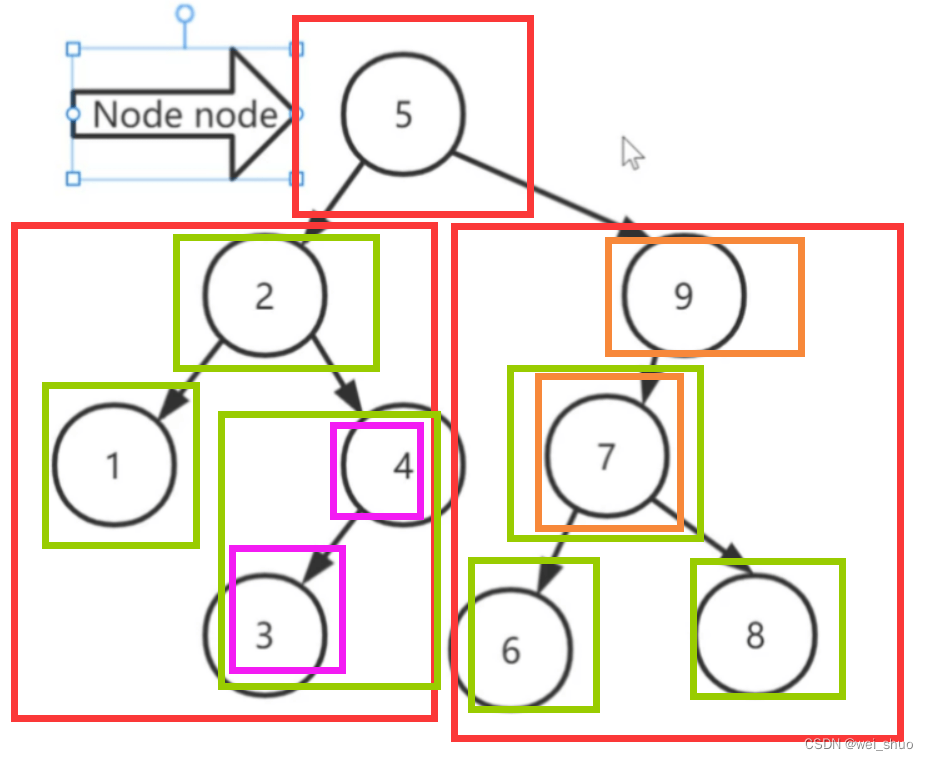
鸡群中至少有三个阶层,分别是公鸡、母鸡和小鸡,每只鸡都有其位置和速度。但区别之处在于,
公鸡最神气,原则上可以随便踱步,只是有的时候注意到其他公鸡的时候,会有抢食的想法,相当于随机抽选一只其他公鸡,对其位置产生影响。母鸡最憋屈,一方面要接受公鸡的领导,另一方面还要和其他母鸡抢食小鸡最无忧无虑,跟着母鸡走就是了。
随着位置关系的变化,母鸡和小鸡可能会逐渐遗忘最初的首领,也就是说种群关系可能会发生变化。
Python实现鸡和鸡群
首先,要实现一个鸡类,一只鸡,有两种基本属性,即位置和类别。
import numpy
as np
from random
import gauss
, random
randint
= np
.random
.randint
uniRand
= np
.random
.uniform
class Chicken:
def __init__(self
, N
, xRange
, order
=0, kind
=0):
# 生成(N)维参数
self
.x
= uniRand
(*xRange
, (N
,))
self
.best
= np
.inf
self
.xBest
= np
.zeros
((N
,))
self
.kind
= kind
# 鸡的类别
self
.order
= order
# 鸡的编号
# 设置自己的首领公鸡
def setCock(self
, i
):
self
.cock
= i
# 设置自己的监护母鸡
def setHen(self
, i
):
self
.hen
= i
其中kind分为三类,分别是公鸡、母鸡和小鸡。其中,每只母鸡都有自己的首领公鸡,每只小鸡都有自己的监护母鸡。
order为这只鸡在鸡群中的编号,主要在鸡群中得以体现。
鸡群和粒子群有一个很大的区别,后者说到底只有一个群,而鸡群中,每个公鸡都有自己的母鸡和小鸡,相当于一个小群体。但鸡和鸡之间的关系,并不取决于鸡自己,故而需要在鸡群中实现
randint
= np
.random
.randint
class Swarm:
# cNum 鸡数,是三个元素的列表,分别是公鸡、母鸡和小鸡数
# N参数维度
def __init__(self
, cNum
, N
, xRange
):
self
.initCs
(cNum
, N
, xRange
)
self
.bestCS
= deepcopy
(self
.cs
) #最佳鸡群
self
.best
= np
.inf
#全局最优值
self
.xBest
= np
.zeros
((N
,)) #全局最优参数
self
.N
= N
def initCs(self
, cNum
, N
, xRange
, vRange
):
self
.cs
= []
self
.cNum
= cNum
self
.cocks
= np
.arange
(cNum
[0]) # 公鸡编号
self
.hens
= np
.arange
(cNum
[0], cNum
[0]+cNum
[1]) #母鸡编号
self
.chicks
= np
.arange
(cNum
[0]+cNum
[1], np
.sum(cNum
)) #小鸡编号
kinds
= np
.repeat
([0,1,2], cNum
)
for i
in range(sum(cNum
)):
self
.cs
.append
(Chicken
(N
,xRange
, vRange
, i
, kinds
[i
]))
if kinds
[i
] > 0:
cock
= randint
(0, cNum
[0])
self
.cs
[i
].setCock
(cock
)
if kinds
[i
] > 1:
hen
= randint
(cNum
[0], cNum
[0]+cNum
[1])
self
.cs
[i
].setHen
(hen
)
鸡群更新
接下来就是算法的核心环节,不同的鸡要遵循不同的更新规则,其中,公鸡最潇洒,其下一步位置只取决于自己,以及另一只随便挑选的公鸡。
公鸡
记当前这只公鸡的编号是i,随机挑选的公鸡编号是j , j≠i,则第i只公鸡位置的更新方法为
xi(t+1)=xi(t)⋅(1+r)
其中,r是通过正态分布生成的随机数,可表示为1∼N(0,σ2),其中σ2为
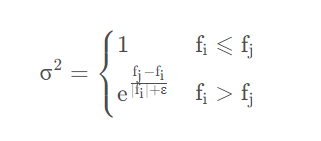
其中f一般叫做适应因子,相当于将某只鸡塞到待搜解的函数中得到的值。例如要搜索y=2的最小值,如果当前这只鸡的位置1.5,那么f=1.52=2.25。ε是一个防止除零错误的小量。
但需要注意,上文中所有的x,表示的并非一个标量,而是一个数组。
其Python实现为
# 写在Swarm类中
def cockStep(self
):
for i
in self
.cocks
:
# 第j只公鸡
j
= np
.random
.randint
(self
.cNum
[0])
if j
==i
:
j
= (j
+1) % self
.cNum
[0]
# 第i只公鸡
ci
= self
.cs
[i
]
# 第j只公鸡
cj
= self
.cs
[self
.cocks
[j
]]
sigma
= 1 if cj
.best
> ci
.best
else np
.exp
(
(cj
.best
–ci
.best
)/(np
.abs(ci
.best
)+1e–15))
ci
.x
*= 1 + gauss
(0, sigma
)
母鸡
设当前母鸡编号为i,这只母鸡既要追随首领公鸡,又要和其他母鸡抢食。
xi(t+1)=xi(t)+k1r1(xc−xi)+k2r2(xj−xi)
其中,xc为其首领公鸡,xj为另一只母鸡或者公鸡。k1,k2为系数,其更新逻辑与公鸡的k是一样的,当fi较大时,表示为
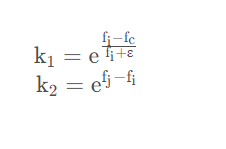
代码实现为:
def henStep(self
):
nGuarder
= self
.cNum
[0] + self
.cNum
[1] – 2
for i
in self
.hens
:
guarders
= list(self
.cocks
) + list(self
.hens
)
c
= self
.cs
[i
].cock
#首领公鸡
guarders
.remove
(i
)
guarders
.remove
(c
)
# 随机生成另一只监护鸡
j
= guarders
[np
.random
.randint
(nGuarder
)]
ci
= self
.cs
[i
]
cj
= self
.cs
[j
]
cc
= self
.cs
[c
]
k1
, k2
= random
(), random
()
if cc
.best
> ci
.best
:
k1
*= np
.exp
((ci
.best
–cc
.best
)/(np
.abs(ci
.best
)+1e–15))
if cj
.best
< ci
.best
:
k2
*= np
.exp
(cj
.best
–ci
.best
)
ci
.x
+= k1
*(cc
.x
–ci
.x
)+k2
*(cj
.x
–ci
.x
)
小鸡
最后是小鸡的更新逻辑,小鸡在母鸡的周围找食物,其更新逻辑为
xi(t+1)=xi(t)+r(xh(t)−xi(t))
其中,xh为其监护母鸡,r为随机数,算法实现为
def chickStep(self
):
for i
in self
.chicks
:
ci
= self
.cs
[i
]
ci
.x
+= 2*random
()*(self
.cs
[ci
.hen
].x
–ci
.x
)
整个鸡群
正所谓,算法源于生活而高于生活,自然界里讲求辈分,但在鸡群算法里,讲究的确是实力。如果小鸡运气爆棚,得到了比公鸡还厉害的优化结果,那么这只小鸡就会进化成公鸡。
也就是说,每隔一段时间,鸡群里的鸡会被重新安排身份,优化效果最好的就是头领公鸡,差一点的是监护母鸡,最差的就只能是小鸡了。
def update(self
):
cn
= np
.sum(self
.cNum
)
c1
, c2
= self
.cNum
[0], self
.cNum
[0]+self
.cNum
[1]
fitness
= [self
.cs
[i
].best
for i
in range(cn
)]
index
= np
.argsort
(fitness
)
self
.cocks
= index
[np
.arange
(c1
)]
self
.hens
= index
[np
.arange
(c1
,c2
)]
self
.chicks
= index
[np
.arange
(c2
,cn
)]
for i
in self
.cocks
:
self
.cs
[i
].kind
= 0
for i
in self
.hens
:
self
.cs
[i
].kind
= 1
for i
in self
.chicks
:
self
.cs
[i
].kind
= 2
for i
in range(cn
):
if self
.cs
[i
].kind
> 0:
cock
= self
.cocks
[randint
(0, c1
)]
self
.cs
[i
].setCock
(cock
)
if self
.cs
[i
].kind
> 1:
hen
= self
.hens
[randint
(c1
,c2
)]
self
.cs
[i
].setHen
(hen
)
优化迭代
至此,集群算法的框架算是搭建成功了,接下来就实现最关键的部分,优化。
其基本逻辑是,输入一个待优化func,通过将每只鸡的位置x带入到这个函数中,得到一个判定值,最后通过这个判定值,来不断更新鸡群。
除了这个函数之外,还需要输入一些其他参数,比如整个鸡群算法的迭代次数,以及鸡群更新的频次等等
# func为待优化函数
# N为迭代次数
# T为鸡群更新周期
def optimize(self
, func
, N
, T
, msgT
):
for n
in range(N
):
# 计算优化参数
for c
in self
.cs
:
c
.best
= func
(c
.x
)
# 分别更新公鸡、母鸡和小鸡
self
.cockStep
()
self
.henStep
()
self
.chickStep
()
if (n
+1)%T
== 0:
self
.update
() #每T次更新一次种群
self
.printBest
(n
)
self
.printBest
(n
)
其中,printBest可以将当前最佳结果打印出来,其形式为
def printBest(self
,n
):
fitness
= [c
.best
for c
in self
.cs
]
best
= np
.min(fitness
)
ind
= np
.where
(fitness
==best
)[0]
msg
= f
“已经迭代{n}次,最佳优化结果为{np.min(fitness)},参数为:n”
msg
+= “, “.join
([f
“{x:.6f}” for x
in self
.cs
[ind
].x
])
print(msg
)
测试
算法完成之后,当然要找个函数测试一下,测试函数为
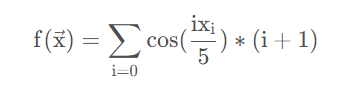
def test(xs
):
_sum
= 0.0
for i
in range(len(xs
)):
_sum
= _sum
+ np
.cos
((xs
[i
]*i
)/5)*(i
+1)
return _sum
if __name__
== “__main__”:
cNum
= [15,20,100]
s
= Swarm
(cNum
, 5, (–5,5))
s
.optimize
(test
, 20, 5)
测试结果如下
已经迭代4次,最佳优化结果为-5.793762423022024,参数为:-6.599526, 3.117137, 5.959538, 7.225785, 5.204990已经迭代9次,最佳优化结果为-10.61594651972434,参数为:-7.003724, -5.589730, 0.981409, 12.920325, -19.006112已经迭代14次,最佳优化结果为-9.143596747975293,参数为:5.388234, -3.714421, -5.254391, -5.216215, -6.079223已经迭代19次,最佳优化结果为-11.097888385616995,参数为:-9.156244, -5.914600, -5.960154, 4.550833, 4.127889已经迭代19次,最佳优化结果为-11.097888385616995,参数为:-9.156244, -5.914600, -5.960154, 4.550833, 4.127889