python实现二分类和多分类的ROC曲线教程

基本概念

precision：预测为对的当中，原本为对的比例（越大越好，1为理想状态）

recall：原本为对的当中，预测为对的比例（越大越好，1为理想状态）

F-measure：F度量是对准确率和召回率做一个权衡（越大越好，1为理想状态，此时precision为1，recall为1）

accuracy：预测对的（包括原本是对预测为对，原本是错的预测为错两种情形）占整个的比例（越大越好，1为理想状态）

fp rate：原本是错的预测为对的比例（越小越好，0为理想状态）

tp rate：原本是对的预测为对的比例（越大越好，1为理想状态）

ROC曲线通常在Y轴上具有真阳性率，在X轴上具有假阳性率。这意味着图的左上角是“理想”点 – 误报率为零，真正的正率为1。这不太现实，但它确实意味着曲线下面积（AUC）通常更好。

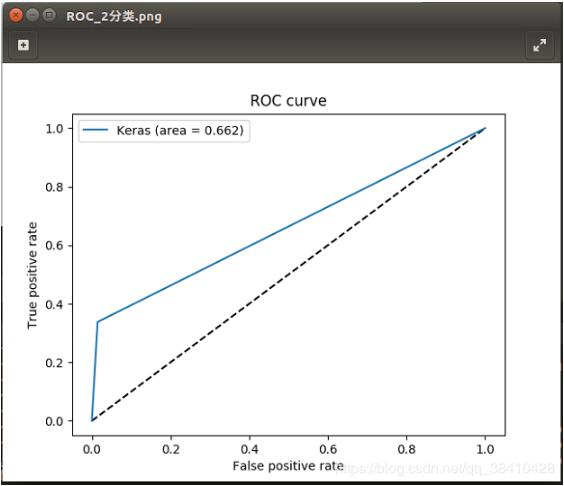
二分类问题：ROC曲线

from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
import time
start_time = time.time()
import matplotlib.pyplot as plt
from sklearn.metrics import roc_curve
from sklearn.metrics import auc
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import recall_score,accuracy_score
from sklearn.metrics import precision_score,f1_score
from keras.optimizers import Adam,SGD,sgd
from keras.models import load_model

print(\'读取数据\')
X_train = np.load(\'x_train-rotate_2.npy\')
Y_train = np.load(\'y_train-rotate_2.npy\')
print(X_train.shape)
print(Y_train.shape)

print(\'获取测试数据和验证数据\')
X_train, X_valid, Y_train, Y_valid = train_test_split(X_train, Y_train, test_size=0.1, random_state=666)

Y_train = np.asarray(Y_train,np.uint8)
Y_valid = np.asarray(Y_valid,np.uint8)
X_valid = np.array(X_valid, np.float32) / 255.

print(\'获取模型\')
model = load_model(\'./model/InceptionV3_model.h5\')
opt = Adam(lr=1e-4)
model.compile(optimizer=opt, loss=\'binary_crossentropy\')

print(\"Predicting\")
Y_pred = model.predict(X_valid)
Y_pred = [np.argmax(y) for y in Y_pred] # 取出y中元素最大值所对应的索引
Y_valid = [np.argmax(y) for y in Y_valid]

# micro：多分类　　
# weighted：不均衡数量的类来说，计算二分类metrics的平均
# macro：计算二分类metrics的均值，为每个类给出相同权重的分值。
precision = precision_score(Y_valid, Y_pred, average=\'weighted\')
recall = recall_score(Y_valid, Y_pred, average=\'weighted\')
f1_score = f1_score(Y_valid, Y_pred, average=\'weighted\')
accuracy_score = accuracy_score(Y_valid, Y_pred)
print(\"Precision_score:\",precision)
print(\"Recall_score:\",recall)
print(\"F1_score:\",f1_score)
print(\"Accuracy_score:\",accuracy_score)

# 二分类　ＲＯＣ曲线
# roc_curve:真正率（True Positive Rate , TPR）或灵敏度（sensitivity）
# 横坐标：假正率（False Positive Rate , FPR）
fpr, tpr, thresholds_keras = roc_curve(Y_valid, Y_pred)
auc = auc(fpr, tpr)
print(\"AUC : \", auc)
plt.figure()
plt.plot([0, 1], [0, 1], \'k--\')
plt.plot(fpr, tpr, label=\'Keras (area = {:.3f})\'.format(auc))
plt.xlabel(\'False positive rate\')
plt.ylabel(\'True positive rate\')
plt.title(\'ROC curve\')
plt.legend(loc=\'best\')
plt.savefig(\"../images/ROC/ROC_2分类.png\")
plt.show()

print(\"--- %s seconds ---\" % (time.time() - start_time))

ROC图如下所示：

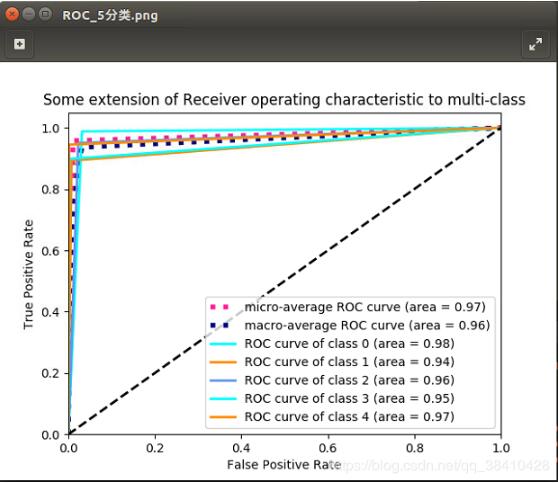
多分类问题：ROC曲线

ROC曲线通常用于二分类以研究分类器的输出。为了将ROC曲线和ROC区域扩展到多类或多标签分类，有必要对输出进行二值化。⑴可以每个标签绘制一条ROC曲线。⑵也可以通过将标签指示符矩阵的每个元素视为二元预测（微平均）来绘制ROC曲线。⑶另一种用于多类别分类的评估方法是宏观平均，它对每个标签的分类给予相同的权重。

from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
import time
start_time = time.time()
import matplotlib.pyplot as plt
from sklearn.metrics import roc_curve
from sklearn.metrics import auc
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import recall_score,accuracy_score
from sklearn.metrics import precision_score,f1_score
from keras.optimizers import Adam,SGD,sgd
from keras.models import load_model
from itertools import cycle
from scipy import interp
from sklearn.preprocessing import label_binarize

nb_classes = 5
print(\'读取数据\')
X_train = np.load(\'x_train-resized_5.npy\')
Y_train = np.load(\'y_train-resized_5.npy\')
print(X_train.shape)
print(Y_train.shape)

print(\'获取测试数据和验证数据\')
X_train, X_valid, Y_train, Y_valid = train_test_split(X_train, Y_train, test_size=0.1, random_state=666)

Y_train = np.asarray(Y_train,np.uint8)
Y_valid = np.asarray(Y_valid,np.uint8)
X_valid = np.asarray(X_valid, np.float32) / 255.

print(\'获取模型\')
model = load_model(\'./model/SE-InceptionV3_model.h5\')
opt = Adam(lr=1e-4)
model.compile(optimizer=opt, loss=\'categorical_crossentropy\')

print(\"Predicting\")
Y_pred = model.predict(X_valid)
Y_pred = [np.argmax(y) for y in Y_pred] # 取出y中元素最大值所对应的索引
Y_valid = [np.argmax(y) for y in Y_valid]

# Binarize the output
Y_valid = label_binarize(Y_valid, classes=[i for i in range(nb_classes)])
Y_pred = label_binarize(Y_pred, classes=[i for i in range(nb_classes)])

# micro：多分类　　
# weighted：不均衡数量的类来说，计算二分类metrics的平均
# macro：计算二分类metrics的均值，为每个类给出相同权重的分值。
precision = precision_score(Y_valid, Y_pred, average=\'micro\')
recall = recall_score(Y_valid, Y_pred, average=\'micro\')
f1_score = f1_score(Y_valid, Y_pred, average=\'micro\')
accuracy_score = accuracy_score(Y_valid, Y_pred)
print(\"Precision_score:\",precision)
print(\"Recall_score:\",recall)
print(\"F1_score:\",f1_score)
print(\"Accuracy_score:\",accuracy_score)

# roc_curve:真正率（True Positive Rate , TPR）或灵敏度（sensitivity）
# 横坐标：假正率（False Positive Rate , FPR）

# Compute ROC curve and ROC area for each class
fpr = dict()
tpr = dict()
roc_auc = dict()
for i in range(nb_classes):
 fpr[i], tpr[i], _ = roc_curve(Y_valid[:, i], Y_pred[:, i])
 roc_auc[i] = auc(fpr[i], tpr[i])

# Compute micro-average ROC curve and ROC area
fpr[\"micro\"], tpr[\"micro\"], _ = roc_curve(Y_valid.ravel(), Y_pred.ravel())
roc_auc[\"micro\"] = auc(fpr[\"micro\"], tpr[\"micro\"])

# Compute macro-average ROC curve and ROC area

# First aggregate all false positive rates
all_fpr = np.unique(np.concatenate([fpr[i] for i in range(nb_classes)]))

# Then interpolate all ROC curves at this points
mean_tpr = np.zeros_like(all_fpr)
for i in range(nb_classes):
 mean_tpr += interp(all_fpr, fpr[i], tpr[i])

# Finally average it and compute AUC
mean_tpr /= nb_classes

fpr[\"macro\"] = all_fpr
tpr[\"macro\"] = mean_tpr
roc_auc[\"macro\"] = auc(fpr[\"macro\"], tpr[\"macro\"])

# Plot all ROC curves
lw = 2
plt.figure()
plt.plot(fpr[\"micro\"], tpr[\"micro\"],
  label=\'micro-average ROC curve (area = {0:0.2f})\'
  \'\'.format(roc_auc[\"micro\"]),
  color=\'deeppink\', linestyle=\':\', linewidth=4)

plt.plot(fpr[\"macro\"], tpr[\"macro\"],
  label=\'macro-average ROC curve (area = {0:0.2f})\'
  \'\'.format(roc_auc[\"macro\"]),
  color=\'navy\', linestyle=\':\', linewidth=4)

colors = cycle([\'aqua\', \'darkorange\', \'cornflowerblue\'])
for i, color in zip(range(nb_classes), colors):
 plt.plot(fpr[i], tpr[i], color=color, lw=lw,
  label=\'ROC curve of class {0} (area = {1:0.2f})\'
  \'\'.format(i, roc_auc[i]))

plt.plot([0, 1], [0, 1], \'k--\', lw=lw)
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel(\'False Positive Rate\')
plt.ylabel(\'True Positive Rate\')
plt.title(\'Some extension of Receiver operating characteristic to multi-class\')
plt.legend(loc=\"lower right\")
plt.savefig(\"../images/ROC/ROC_5分类.png\")
plt.show()

print(\"--- %s seconds ---\" % (time.time() - start_time))

ROC图如下所示：